Twinning (CCP4: General)

NAME

PLEASE NOTE: Most of this document has been taken directly from chapter 6 of the SHELX-97 Manual.

Contents

• Introduction
• The warning signs for twinning
• Examples
• Frequently encounted twin laws
• Likely twinning operators
  • General Remarks
  • Lookup tables

Introduction

A typical definition of a twinned crystal is the following: "Twins are regular aggregates consisting of crystals of the same species joined together in some definite mutual orientation" (Giacovazzo, 1992). For this to happen two lattice repeats in the crystal must be of equal length to allow the array of unit cells to pack compactly. The result is that the reciprocal lattice diffracted from each component will overlap, and instead of measuring only I_hkl from a single crystal, the experiment yields
k_m I_hkl(crystal₁) + (1-k_m) I_h'k'l'(crystal₂)

For a description of a twin it is necessary to know the matrix that transforms the hkl indices of one crystal into the h'k'l' of the other, and the value of the fractional component k_m. Those space groups where it is possible to index the cell along different axes are also very prone to twinning.

When the diffraction patterns from the different domains are completely superimposable, the twinning is termed merohedral. The special case of just two distinct domains (typical for macromolecules) is termed hemihedral. When the reciprocal lattices do not superimpose exactly, the diffraction pattern consists of two (or more) interpenetrating lattices, which can in principle be separated. This is termed non-merohedral or epitaxial twinning.

The warning signs for twinning

Experience shows that there are a number of characteristic warning signs for twinning. Of course not all of them can be present in any particular example, but if one finds several of them, the possibility of twinning should be given serious consideration.

1. The metric symmetry is higher than the Laue symmetry.
2. The R_merge-value for the higher symmetry Laue group is only slightly higher than for the lower symmetry Laue group.
3. The mean value for |E²-1| is much lower than the expected value of 0.736 for the non-centrosymmetric case. If we have two twin domains and every reflection has contributions from both, it is unlikely that both contributions will have very high or that both will have very low intensities, so the intensities will be distributed so that there are fewer extreme values. This can be seen by plotting the output of TRUNCATE or ECALC.
4. The space group appears to be trigonal or hexagonal.
5. There are impossible or unusual systematic absences.
6. Although the data appear to be in order, the structure cannot be solved.
7. The Patterson function is physically impossible.

The following points are typical for non-merohedral twins, where the reciprocal lattices do not overlap exactly and only some of the reflections are affected by the twinning:

8. There appear to be one or more unusually long axes, but also many absent reflections.
9. There are problems with the cell refinement.
10. Some reflections are sharp, others split.
11. K=mean(F_o²)/mean(F_c²) is systematically high for the reflections with low intensity.
12. For all of the 'most disagreeable' reflections, F_o is much greater than F_c.

Examples

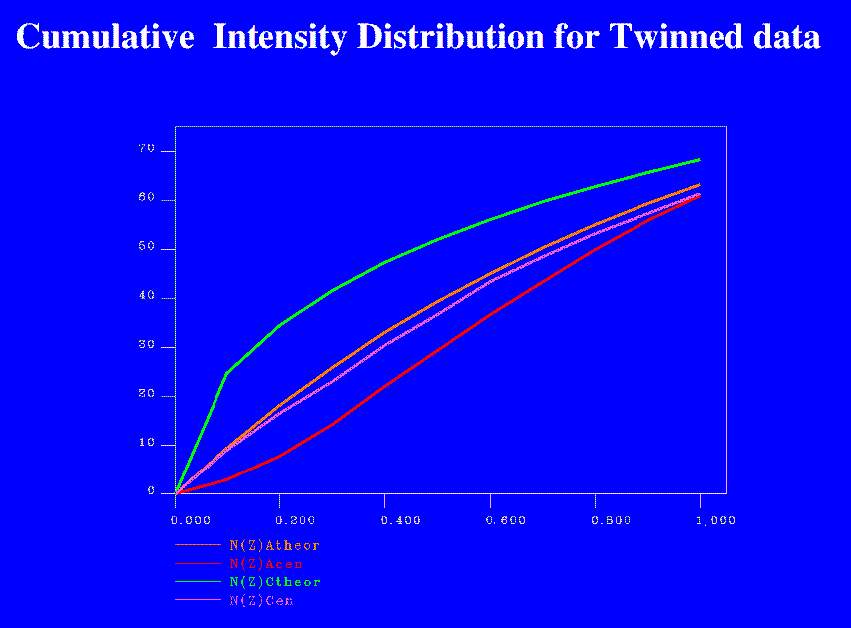
Example of a cumulative intensity distribution with twinning present, as plotted by TRUNCATE. (A full size version of the example can be viewed by clicking on the small picture.)

Cumulative intensity distribution for twin

Frequently encountered twin laws

The following cases are relatively common:

1. Twinning by merohedry. The lower symmetry trigonal, rhombohedral, tetragonal, hexagonal or cubic Laue groups may be twinned so that they look (more) like the corresponding higher symmetry Laue groups (assuming the c-axis unique except for cubic)
2. Orthorhombic with a and b approximately equal in length may emulate tetragonal
3. Monoclinic with beta approximately 90° may emulate orthorhombic:
4. Monoclinic with a and c approximately equal and beta approximately 120° may emulate hexagonal [P2₁/c would give absences and possibly also intensity statistics corresponding to P6₃].
5. Monoclinic with na + nc ~ a or na + nc ~ c can be twinned. See HIPIP examples.

Likely twinning operators

General Remarks

A crystal is a 3-dimensional translational repeat of a structural pattern which may comprise a molecule, part of a symmetric molecule, or several molecules. The repeats which can overlap by simple translation, are called unit cells.

Lattice symmetry enforces extra limitations. There are 7 basic symmetry classes possible within a crystal:

Triclinic - no rotational symmetry. No restrictions on a b c or alpha beta gamma

Monoclinic - one 2 fold axis of rotation - two angles must be 90; usually alpha and Gamma.

Orthorhombic - two perpendicular 2 fold axes of rotation (these must generate a 3rd) All angles 90.

Tetragonal - one 4 fold axis of rotation (plus possible perpendicular 2-fold). All angles 90; a = b.

Trigonal - one 3 fold axis of rotation (plus possible perpendicular 2-folds). Alpha and Beta = 90, Gamma = 120 ; a = b (hexagonal setting).

Hexagonal - one 6 fold axis of rotation (plus possible perpendicular 2-fold). Alpha and Beta = 90, Gamma = 120 ; a = b.

Cubic - all axes equal and equivalent, related by a diagonal 3-fold; also 2-fold, or 4-fold axes of rotation along crystal axes. All angles 90 ; a = b = c

Problems arise most commonly when two or more crystal axes are the same length, either by accident in the monoclinic and orthorhombic system, or as a requirement of the symmetry as in the tetragonal, trigonal, hexagonal or cubic systems.

Although the a and b axes in the tetragonal, trigonal, hexagonal and cubic classes must be equal in length, there can still be ambiguities in their definition, and consequentially in the indexing of the diffraction pattern. It is these classes of crystals which are most prone to twinning.

monoclinic

It is possible that in P21 or C2 there are two possible choices of a with anew = aold + ncold. If the magnitude of a is equal to that of a+nc, the cos rule requires that cos(Beta*) = |nc|/2|a|, or, if |a|>|c|, cos(Beta*) = |na|/2|c|.

orthorhombic

For orthorhombic crystal forms the only possibility for twinning is if there are two axes with nearly the same length.

tetragonal, trigonal, hexagonal, cubic

For tetragonal, trigonal, hexagonal or cubic systems it is a requirement of the symmetry that two cell axes are equal. Assuming the lengths of a and b to be equal, and maintaining a right-handed axial system, we find:

For these spacegroups the real axial system could be:	(a,b,c)	or	(-a,-b,c)	or	(b,a,-c)	or	(-b,-a,-c)
with corresponding reciprocal axes:	(a*,b*,c*)	or	(-a*,-b*,c*)	or	(b*,a*,-c*)	or	(-b*,-a*,-c*)
Corresponding indexing systems:	(h,k,l)	or	(-h,-k,l)	or	(k,h,-l)	or	(-k,-h,-l)

In these cases, any of the above definitions of axes is equally valid. For many cases the alternative systems are symmetry equivalents, and hence do not generate detectable differences in the diffraction pattern. But for crystals where this is not true, twinning is possible. Different domains may have different definitions of axes, which lead to different diffraction intensities superimposed on the same lattice.

Lookup tables for tetragonal, trigonal, hexagonal, cubic

Here are details for the possible systems. These tables are generated by considering each of the indexing systems above, and eliminating those which correspond to symmetry operators of the spacegroup. While twinning involves more than one indexing possibility within a single dataset, these operators are also relevant for ensuring the same indexing between multiple datasets when there is no twinning.

• All P4i and related 4i space groups:
  (h,k,l) equivalent to (-h,-k,l) so we only need to check:

  real axes:	(a,b,c)	and	(b,a,-c)
  reciprocal axes:	(a*,b*,c*)	and	(b*,a*,-c*)

  When more than one dataset, check if reindexing (h,k,l) to (k,h,-l) gives a better match to previous data sets.
• Twinning possible with this operator - apparent Laue symmetry for perfect twin would be P422

space group number	space group	point group	possible twin operator
75	P4	PG4	k,h,-l
76	P41	PG4	k,h,-l
77	P42	PG4	k,h,-l
78	P43	PG4	k,h,-l
79	I4	PG4	k,h,-l
80	I41	PG4	k,h,-l



• For all P4i2i2 and related 4i2i2 space groups:
  (h,k,l) is equivalent to all of (-h,-k,l) , (k,h,-l) and (-k,-h,-l) so all axial pairs are already equivalent as a result of the crystal symmetry.
• No twinning possible but a perfect twin for the Laue group P4 might appear to have this symmetry.

space group number	space group	point group	no twin operators
89	P422	PG422	none
90	P4212	PG422	none
91	P4122	PG422	none
92	P41212	PG422	none
93	P4222	PG422	none
94	P42212	PG422	none
95	P4322	PG422	none
96	P43212	PG422	none
97	I422	PG422	none
98	I4122	PG422	none



• All P3i and H3:
  (h,k,l) neither equivalent to (-h,-k,l) nor (k,h,-l) nor (-k,-h,-l) so we need to check all 4 possibilities. These are the only cases where tetratohedral twinning can occur:

  real axes:	(a,b,c)	and	(-a,-b,c)	and	(b,a,-c)	and	(-b,-a,c)
  reciprocal axes:	(a*,b*,c*)	and	(-a*,-b*,c*)	and	(b*,a*,-c*)	and	(-b*,-a*,c*)

  i.e. For P3, consider reindexing (h,k,l) to (-h,-k,l) or (k,h,-l) or (-k,-h,-l).
  

  For H3 the indices must satisfy the relationship -h +k+l =3n so it is only possible to reindex as ( k, h,-l). Note that the latter is a symmetry operator of H32, so that twinning is not possible in H32. However, twinning in H3 may give apparent H32 symmetry.

  For trigonal space groups, symmetry equivalents do not seem as "natural" as in other systems. Replacing the 4 basic sets with other symmetry equivalents gives a bewildering range of apparent possibilities, but all are equivalent to one of the above.

  Two-fold twinning possible with this operator - apparent Laue symmetry for two fold perfect twin could be P321 (operator k,h,-l) or P312 (operator -k,-h,-l) or P6 (operator -h,-k,l) Four-fold twinning with these operators could generate apparent Laue symmetry of P622

  space group number	space group	point group	possible twin operators
  143	P3	PG3	-h,-k,l; k,h,-l; -k,-h,-l
  144	P31	PG3	-h,-k,l; k,h,-l; -k,-h,-l
  145	P32	PG3	-h,-k,l; k,h,-l; -k,-h,-l
  146	H3	PG3	k,h,-l

  
  
• All P3i12:
  (h,k,l) already equivalent to (-k,-h,-l) so we only need to check:

  real axes:	(a,b,c)	and	(b,a,-c)
  reciprocal axes:	(a*,b*,c*)	and	(b*,a*,-c*)

  i.e. reindex (h,k,l) to (k,h,-l) [or its equivalent operator (-h,-k,l)].
• Twinning possible with this operator - apparent symmetry for two fold perfect twin would be P622 (operator -h,-k,l)

space group number	space group	point group	possible twinning operator
149	P312	PG312	-h,-k,l or k,h,-l
151	P3112	PG312	-h,-k,l or k,h,-l
153	P3212	PG312	-h,-k,l or k,h,-l



• All P3i21:
  (h,k,l) already equivalent to (k,h,-l) so we only need to check:

  real axes:	(a,b,c)	and	(-a,-b,-c)
  reciprocal axes:	(a*,b*,c*)	and	(-a*,-b*,-c*)

  i.e. reindex (h,k,l) to (-h,-k,l) [or its equivalent operator (-k,-h,-l)].
• Twinning possible with this operator - apparent symmetry for two fold perfect twin would be P622 (operator -h,-k,l)

space group number	space group	point group	possible twinning operator
150	P321	PG321	-h,-k,l or -k,-h,-l
152	P3121	PG321	-h,-k,l or -k,-h,-l
154	P3221	PG321	-h,-k,l or -k,-h,-l



• All P6i:
  (h,k,l) already equivalent to (-h,-k,l) so we only need to check:

  real axes:	(a,b,c)	and	(b,a,-c)
  reciprocal axes:	(a*,b*,c*)	and	(b*,a*,-c*)

  i.e. reindex (h,k,l) to (k,h,-l).
• Twinning possible with this operator - apparent symmetry for two fold perfect twin would be P622 (operator k,k,-l)

  space group number	space group	point group	possible twinning operator
  168	P6	PG6	k,h,-l
  169	P61	PG6	k,h,-l
  170	P65	PG6	k,h,-l
  171	P62	PG6	k,h,-l
  172	P64	PG6	k,h,-l
  173	P63	PG6	k,h,-l

  
  
• All P6i22:
  (h,k,l) already equivalent to (-h,-k,l) and (k,h,-l) and (-k,-h,-l) so no twinning possible. However a perfect twin for the Laue group, P312, P321 or P6 might appear to have this symmetry.

space group number	space group	point group	no twinning operator
177	P622	PG622	none
178	P6122	PG622	none
179	P6522	PG622	none
180	P6222	PG622	none
181	P6422	PG622	none
182	P6322	PG622	none



• All P2i3 and related 2i3 space groups:
  (h,k,l) already equivalent to (-h,-k,l) so we only need to check:

  real axes:	(a,b,c)	and	(b,a,-c)
  reciprocal axes:	(a*,b*,c*)	and	(b*,a*,-c*)

  i.e. reindex (h,k,l) to (k,h,-l).
• Twinning possible with this operator - apparent symmetry for two fold perfect twin would be P43 (operator k,h,-l)

  space group number	space group	point group	possible twinning operator
  195	P23	PG23	k,h,-l
  196	F23	PG23	k,h,-l
  197	I23	PG23	k,h,-l
  198	P213	PG23	k,h,-l
  199	I213	PG23	k,h,-l

  
  
• All P4i32 and related 4i32 space groups:
  (h,k,l) already equivalent to (-h,-k,l) and (k,h,-l) and (-k,-h,-l) so we do not need to check.

space group number	space group	point group	no twinning operator
207	P432	PG432	none
208	P4232	PG432	none
209	F432	PG432	none
210	F4132	PG432	none
211	I432	PG432	none
212	P4332	PG432	none
213	P4132	PG432	none
214	I4132	PG432	none

SEE ALSO

More information on twinning can be found at: Fam and Yeates' Introduction to Hemihedral Twinning, which includes a Twinning test.

AUTHORS

Acknowledgement in SHELX manual:

"I should like to thank Regine Herbst-Irmer
            who wrote most of this chapter."

Prepared for CCP4 by Maria Turkenburg, University of York, England